pH jumpのお気持ちを探る

きれないはさみ

1 概要

　中和滴定において, 当量点でみられるpHの大きな変化をpH jumpといいます。中和滴定でpH jumpが起きることは高校化学において基本的な事項ですが, 筆者は高校時代このpH jumpがどうにも腑に落ちなかったので, この場を借りて考えてみようと思います。(需要あるのかな...)

　分析の方法ですが, モル濃度\(c_a\)で体積\(V\)の酸にモル濃度\(c_b\)の水酸化ナトリウム水溶液(強塩基)を滴下する場合に対して, 滴下した分の体積\(v\)(ただし, 簡単のため \(x=\dfrac{v}{V}\)を\(v\)の代わりに用いる)とpH(または\([\mathrm{H}^+]\))の理論上の関係を数式やグラフ作成ソフト(GeoGebra)を用いて分析する, という感じでやっていこうかと思います。

2 pH jumpの簡易的な説明

　まずは一価の強酸に対して以下の簡単な式(2.1),(2.2)から考えてみます。

\begin{equation} [\mathrm{H}^+]= \begin{cases} c_a-\dfrac{c_bv}{V}=c_a-c_bx&\left(x<\dfrac{c_a}{c_b}\right)\\ \dfrac{K_w}{\frac{v_bv}{V}-c_a}=\dfrac{K_w}{c_bx-c_a}&\left(x>\dfrac{c_a}{c_b}\right) \end{cases}\tag{2.1} \end{equation} \begin{equation} \mathrm{pH}= \begin{cases} -\log_{10}(c_a-c_bx)&\left(x<\dfrac{c_a}{c_b}\right)\\ \log_{10}(c_b-c_a)-\log_{10}K_w&\left(x>\dfrac{c_a}{c_b}\right) \end{cases}\tag{2.2} \end{equation}

(2.2)は単に対数関数を2つ組み合わせたものであり \(x→c_a / c_b ±0\) で発散するため, pH jumpは対数関数の発散に相当する, と簡単にpH jumpを説明できます。

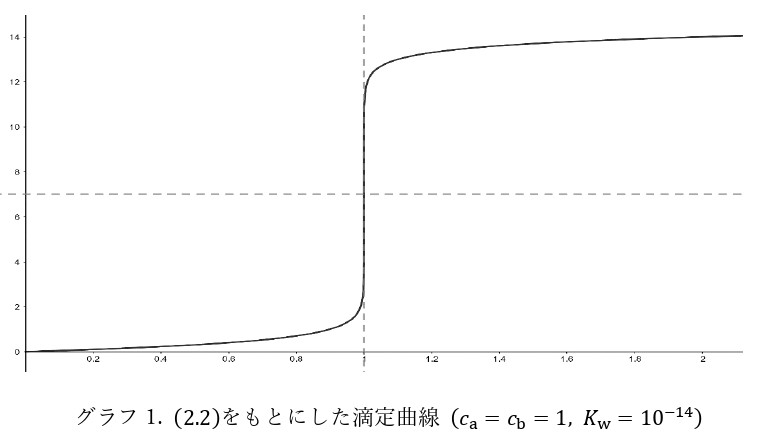
　(2.1),(2.2)はわかりやすい反面 ①滴下による体積の増加 ②当量点前での\([\mathrm{H}^+]\)と\([\mathrm{OH}^-]\)の化学平衡 などが無視されており, 粗いモデルだといえそうです。また, 弱酸や多価の酸などを用いる場合の滴定曲線の振る舞いはこれだけだとわかりません。以下では①, ②を無視せず, かつ一価の強酸に限らず種々の酸を用いる場合について考えます。

3　一価強酸-一価強塩基での中和反応

用いる酸が一価の強酸HAである場合を考えます。電荷のつり合いや水のイオン積などから, 各イオンについて次式が成り立ちます。(ただし \(\sqrt{K_w}\ll c_a ,c_b\))

\begin{equation} \begin{cases} [\mathrm{Na}^+]+[\mathrm{H^+}]=[\mathrm{A}^-]+[\mathrm{OH}^-]\\ [\mathrm{H}^+][\mathrm{OH}^-]=K_w\\ [\mathrm{Na}^+]=\dfrac{c_bv}{V+v}=\dfrac{c_bx}{1+x}\\ [\mathrm{A}^-]=\dfrac{c_aV}{V+v}=\dfrac{c_a}{1+x} \end{cases}\tag{3.1} \end{equation}

(3.1)から\([\mathrm{H}^+]\)以外のイオン濃度の項を削除して\([\mathrm{H}^+]\)について解くと

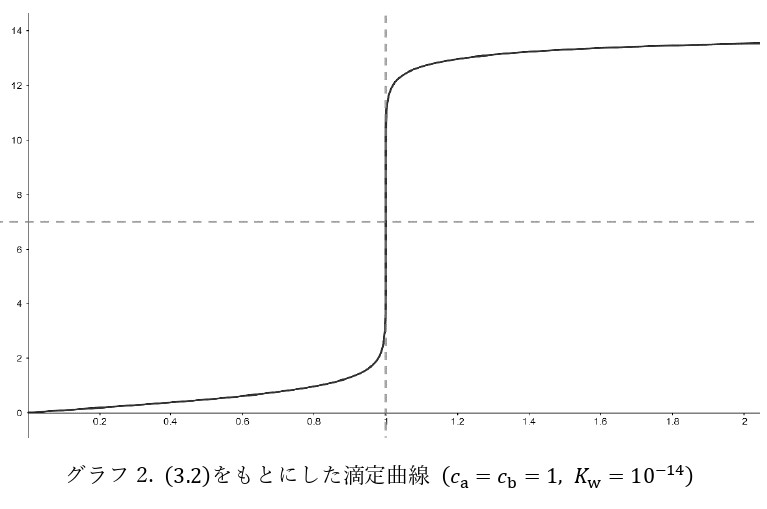
\begin{equation} [\mathrm{H}^+]=\dfrac{c_a-c_bx+\sqrt{(c_a-c_bx)^2+4K_w(1+x)^2}}{2(1+x)}\tag{3.2} \end{equation}

ところで, \(\mathrm{pH}=-\log_{10}[\mathrm{H}^+]\) なので次式が一般に成り立ちます。

\begin{equation} \dfrac{d\mathrm{pH}}{dx}=-\dfrac{1}{[\mathrm{H}^+]}\cdot\dfrac{d[\mathrm{H}^+]}{dx}\cdot\log_{10}e\propto-\dfrac{1}{[\mathrm{H}^+]}\cdot\dfrac{d[\mathrm{H}^+]}{dx}\tag{3.3} \end{equation}

したがって, 当量点で滴定曲線の傾き \(-\dfrac{1}{[\mathrm{H^+}]}⋅\dfrac{d[\mathrm{H^+}]}{dx}\) が極大になればpH jumpが起こることが示せます。

　さて, 強酸-強塩基中和滴定に話を戻すと

\begin{equation} -\dfrac{1}{[\mathrm{H}^+]}\cdot\dfrac{d[\mathrm{H}^+]}{dx}=\frac{c_b}{\sqrt{(c_a-c_bx)+4K_w}}+\frac{1}{1+x}\tag{3.4} \end{equation}

第二項は第一項と比べて変化が大きくないと期待できるので, \(-\dfrac{1}{[\mathrm{H^+}]}⋅\dfrac{d[\mathrm{H^+}]}{dx}\)の大小は第一項の大小で主に決定すると考えられます。第一項が最大になるのは\(x=c_a / c_b\), すなわち当量点です。こうしてpH jumpが起きることが示されました。

ちなみに, 当量点における滴定曲線の傾きは

\begin{equation} -\dfrac{1}{[\mathrm{H}^+]}\cdot\left.\dfrac{d[\mathrm{H}^+]}{dx}\right|_{x=\frac{c_a}{c_b}}\cong\dfrac{c_b}{2\sqrt{K_w}}\tag{3.5} \end{equation}

\(\sqrt{K_w}\ll c_b\) と(3.5)より, 強酸-強塩基中和滴定のpH jumpはかなり鋭くなると予想できます。

4　一価弱酸-一価強塩基での中和反応

　今度は用いる酸が一価で電離定数\(K_a\)の弱酸HAである場合を考えます。3.と同様に(4.1)で立式して\([\mathrm{H}^+]\)以外のイオン濃度項を削除すると(4.2)が得られます。(ただし\(\sqrt{K_w}< K_a\ll c_a,c_b\))

\begin{equation} \begin{cases} [\mathrm{Na}^+]+[\mathrm{H^+}]=[\mathrm{A}^-]+[\mathrm{OH}^-]\\ [\mathrm{H}^+][\mathrm{OH}^-]=K_w\\ [\mathrm{Na}^+]=\dfrac{c_bv}{V+v}=\dfrac{c_bx}{1+x}\\ [\mathrm{A}^-]=\dfrac{c_aV}{V+v}=\dfrac{c_a}{1+x}\\ K_a=\dfrac{[\mathrm{A}^-][\mathrm{H}^+]}{[\mathrm{HA}]} \end{cases}\tag{4.1} \end{equation} \begin{equation} x=\dfrac{-[\mathrm{H}^+]^3-K_a[\mathrm{H}^+]^2+(K_w+K_ac_a)[\mathrm{H}^+]+K_aL_w}{(K_a+[\mathrm{H^+}])([\mathrm{H}^+]^2+c_b[\mathrm{H}^+]-K_w)}\tag{4.2} \end{equation}

(3.2)と比べて(4.2)はずいぶんと複雑になってしまったので, 近似をうまく使う必要がありそうです。\([\mathrm{H}^+]\ll K_a\)を仮定して(4.2)の右辺の分母と分子でそれぞれ微小な項を無視すると

\begin{equation} x=\dfrac{-\bcancel{[\mathrm{H}^+]^3}-\bcancel{K_a[H^+]^2}+(K_w+K_ac_a)[\mathrm{H}^+]+K_aK_w}{\bcancel{[\mathrm{H}^+]^3}+(K_a+c_b)[\mathrm{H}^+]^2+(K_ac_b-\bcancel{K_w})[\mathrm{H^+}]-K_aK_w}\cong\dfrac{K_ac_a[\mathrm{H^+}]+K_aK_w}{c_b[\mathrm{H}^+]^2+K_ac_b[\mathrm{H}^+]-K_aK_w}\tag{4.4} \end{equation}

\(x=c_a/c_b\)のとき(4.3)を\([\mathrm{H}^+]\)について解くと

\begin{equation} [\mathrm{H}^+]=\sqrt{\dfrac{K_aK_w(c_a+c_b)}{c_ac_b}}\ (\ll K_a)\tag{4.4} \end{equation}

(4.4)は当量点の水素イオン濃度を表すといえそうです。

ところで, (4.3)を\([\mathrm{H}^+]\)で微分すると

\begin{equation} \dfrac{dx}{d[\mathrm{H}^+]}=-\dfrac{K_a(c_ac_b[\mathrm{H}^+]^2+2K_wc_b[\mathrm{H}^+]+K_aK_w(c_a+c_b))}{(c_b[\mathrm{H}^+]^2+K_ac_b[\mathrm{H}^+]-K_aK_w)^2}\tag{4.5} \end{equation}

(4.4)より当量点付近では\(c_b[\mathrm{H}^+]\gg K_w\)なので

\begin{equation} \dfrac{dx}{d[\mathrm{H}^+]}=-\dfrac{K_a(c_ac_b[\mathrm{H}^+]^2+\bcancel{2K_wc_b[\mathrm{H}^+]}+K_aK_w(c_a+c_b))}{(\bcancel{c_b[\mathrm{H}^+]^2}+K_ac_b[\mathrm{H}^+]-\bcancel{K_aK_w})^2}=-\dfrac{c_ac_b[\mathrm{H}^+]^2+K_aK_w(c_a+c_b)}{K_ac_b^2[\mathrm{H}^+]^2}\tag{4.6} \end{equation} \begin{equation} -\dfrac{1}{[\mathrm{H}^+]}\cdot\dfrac{d[\mathrm{H}^+]}{dx}=\dfrac{K_ac_b^2[\mathrm{H}^+]}{c_ac_b[\mathrm{H}^+]^2+K_aK_w(c_a+c_b)}=\dfrac{K_ac_b^2}{c_ac_b[\mathrm{H}^+]+\dfrac{K_aK_w(c_a+c_b)}{[\mathrm{H}^+]}}\tag{4.7} \end{equation}

(4.4),(4.7)より\(-\dfrac{1}{[\mathrm{H}^+]}\cdot\dfrac{d[\mathrm{H}^+]}{dx}\)はやはり当量点で最大となり, したがってpH jumpが起こると示されました。

ちなみに, 当量点における滴定曲線の傾きは

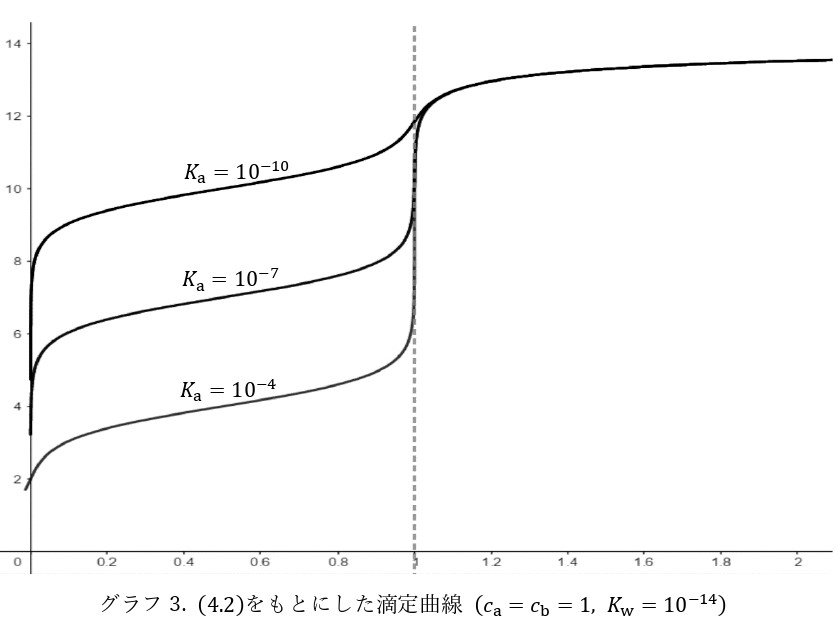
\begin{equation} -\dfrac{1}{[\mathrm{H}^+]}\cdot\left.\dfrac{d[\mathrm{H}^+]}{dx}\right|_{x=\frac{c_a}{c_b}}\cong\dfrac{1}{2}\cdot\sqrt{\dfrac{K_ac_b^3}{K_wc_a(c_a+c_b)}}\tag{4.8} \end{equation}

(4.8)から, 直感通り\(K_a\)が大きい(つまり酸が強い)ほどpH jumpが顕著になることが読み取れます。また, (3.5)と(4.8)を比較することで弱酸-強塩基中和滴定は強酸-強塩基中和滴定ほどpH jumpが鋭くないと予想できます。

5 二価弱酸-一価強塩基での中和反応

最後に, 用いる酸が二価で電離定数が\(K_1,K_2(K_1>K_2)\)の弱酸\(\mathrm{H_2A}\)である場合を考えます。3, 4と同様に(5.1)から\([\mathrm{H}^+]\)以外のイオン濃度項を削除すると(5.2)が得られます。(ただし\(K_2\ll K_1\ll c_a,c_b,\),\(K_w\ll c_a,c_b\) )

\begin{equation} \begin{cases} [\mathrm{Na}^+]+[\mathrm{H}^+]=[\mathrm{HA}^-]+2[\mathrm{A}^{2-}]+[\mathrm{OH}^-]\\ [\mathrm{H}^+][\mathrm{OH}^-]=K_w\\ [\mathrm{Na}^+]=\dfrac{c_bx}{1+x}\\ [\mathrm{H_2A}]+[\mathrm{HA}^-]+[\mathrm{A}^{2-}]=\dfrac{c_a}{1+x}\\ K_1=\dfrac{[\mathrm{HA}^-][\mathrm{H}^+]}{[\mathrm{H_2A}]}\\ K_2=\dfrac{[\mathrm{A}^{2-}][\mathrm{H}^+]}{[\mathrm{HA}^-]} \end{cases}\tag{5.1} \end{equation}

\([\mathrm{H}^+]\gg K_2\)と仮定すると

\begin{align} x&=\dfrac{-[\mathrm{H}^+]^3-K_1[\mathrm{H}^+]^2+(K_w+K_1c_a)[\mathrm{H}^+]^2+(K_w+2K_2c_a)K_1[\mathrm{H}^+]-\bcancel{K_1K_2[\mathrm{H}^+]^2}+\bcancel{K_1K_2K_w}}{(\bcancel{K_1K_2}+K_1[\mathrm{H}^+]+[\mathrm{H}^+]^2)([\mathrm{H}^+]^2+c_b[\mathrm{H}^+]-K_w)}\\ &\cong\dfrac{-[\mathrm{H}^+]^3-K_1[\mathrm{H}^+]^2+(K_w+K_1c_a)[\mathrm{H}^+]^2+K_1(K_w+2K_2c_a)}{(K_1[\mathrm{H}^+]+[\mathrm{H}^+]^2)([\mathrm{H}^+]^2+c_b[\mathrm{H}^+]-K_w)}\tag{5.3} \end{align}

(4.2)によく似た形に変形できました。したがって, 3. と同様当量点\(x=c_a/c_b\)でpH jumpが起きそうです。また, このときの水素イオン濃度と滴定曲線の傾きも3 と同様に考えられます。

\begin{equation} [\mathrm{H}^+]=\sqrt{\dfrac{K_1(K_w+2K_2c_a)(c_a+c_b)}{c_ac_b}}\ (\gg K_2)\tag{5.4} \end{equation} \begin{equation} -\dfrac{1}{[\mathrm{H}^+]}\cdot\left.\dfrac{d[\mathrm{H}^+]}{dx}\right|_{x=\frac{c_a}{c_b}}\cong\dfrac{1}{2}\sqrt{\dfrac{K_1c_b^3}{(K_w+2K_2c_a)c_a(c_a+c_b)}}\tag{5.5} \end{equation}

(5.5)から, 酸の電離定数が同じだとしても二段階目の電離があるとpH jumpが鈍くなる, と読み取れます。

今度は\([\mathrm{H}^+]\ll K_1\)と仮定すると

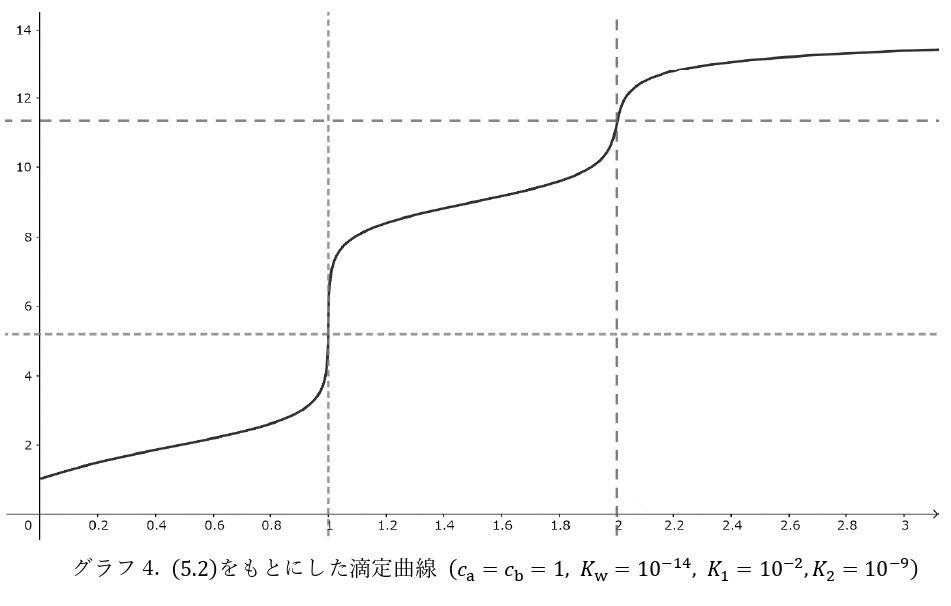
\begin{align} x&=\dfrac{-K_1[\mathrm{H}^+]^3-K_1K_2[\mathrm{H}^+]^2+(K_wK_1+K_1+K_2c_a)[\mathrm{H}^+]+K_1K_2K_w-[\mathrm{H}^+]^4+(K_w+K_1c_a)[\mathrm{H}^+]^2+K_1K_2c_a[\mathrm{H}^+]}{(K_1K_2+K_1[\mathrm{H}^+]+[\mathrm{H}^+]^2)([\mathrm{H}^+]^2+c_b[\mathrm{H}^+]-K_w)}\\ &=\dfrac{-[\mathrm{H}^+]^3-K_2[\mathrm{H}^+]^2+(K_w+K_2c_a)[\mathrm{H}^+]+K_2K_w}{\left(K_2+[\mathrm{H}^+]+\frac{\bcancel{[\mathrm{H}^+]^2}}{\bcancel{K_1}}\right)([\mathrm{H}^+]+c_b[\mathrm{H}^+]-K_w)}+\dfrac{(K_1[\mathrm{H^+}]^2+K_1K_2)c_a-\bcancel{[\mathrm{H}^+]^4}+\bcancel{K_w[\mathrm{H}^+]^2}}{(K_1K_2+K_1[\mathrm{H}^+]+\bcancel{[\mathrm{H}^+]^2})(\bcancel{[\mathrm{H}^+]^2}+c_b[\mathrm{H}^+]-\bcancel{K_w})}\\ &\cong\dfrac{-[\mathrm{H}^+]^3-K_2[\mathrm{H}^+]^2+(K_w+K_2c_a)[\mathrm{H}^+]+K_2K_w}{(K_2+[\mathrm{H}^+])([\mathrm{H}^+]^2+c_b[\mathrm{H}^+]-K_w)}+\dfrac{c_a}{c_b}\tag{5.6} \end{align}

こちらも(4.2)によく似た形に変形できました。今度は当量点\(x\equiv2c_a/c_b\)でpH jumpが起きそうです。また, このときの水素イオン濃度と滴定曲線の傾きも当量点\(x=2c_a/c_b\)と同様に考えることができます。

\begin{equation} [\mathrm{H}^+]=\sqrt{\dfrac{K_2K_w(c_a+c_b)}{c_ac_b}}\ (\ll K_1)\tag{5.7} \end{equation} \begin{equation} -\dfrac{1}{[\mathrm{H}^+]}\cdot\left.\dfrac{d[\mathrm{H}^+]}{dx}\right|_{x=\frac{2c_a}{c_b}}\cong\dfrac{1}{2}\sqrt{\dfrac{K_2c_b^2}{K_wc_b(c_a+c_b)}}\tag{5.8} \end{equation}

最後までお読みいただきありがとうございました。