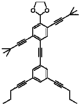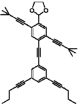
奇妙な芳香族
勉 座明
かなりの長文となっています。適当に興味のある部分だけつまみ食いしてください。1,2章はすっ飛ばして本題の3章に行くのもありだと思います。
目次
1. 導入2. 芳香族とは?
2.1. 芳香族とは?
2.2. Hückel則とは
2.3. 種々の物差し
2.4. 総合して、現在の芳香族とは?
3. 奇妙な芳香族
3.1. ホモ芳香族
3.1. Möbius(メビウス)芳香族
3.3. 三次元芳香族
3.4. その他
4. 最後に
5. 付録
5.1. LCAO近似と永年方程式
5.2. Hückel則の導出
5.3. Möbius則の導出
1. 導入
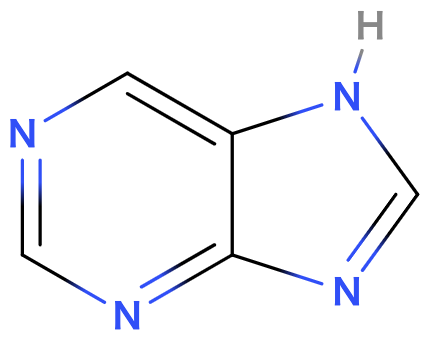
「芳香族」。高校・大学などで有機化学に触れたことがある人であれば、誰もが聞き覚えがある言葉だと思います。 ですが芳香族と言われたときに、その言葉が意味するものは何なのかと問うとその答えは大きく2つに分かれると思います。1つはベンゼン環を持つというもの。もう1つはHückel則を満たすというもの。 この答えを探るために、まずはどのようにして芳香族とその他化合物が分けられるのかについての紹介をします。 その後にタイトルの通り、多くの人の感覚からずれた「奇妙」にも思える芳香族について、 いくつか紹介させていただきます。 本文中に数式の計算とか変形は基本的に出しません。数式を用いる部分は全て付録(つまり読まなくても良い)に回しています。

2. 芳香族とは?
2.1. 芳香族についての歴史
芳香族が何を指すのか?それを探るためにまず、芳香族に関しての歴史について重要な点を抑えてまとめてみましょう。


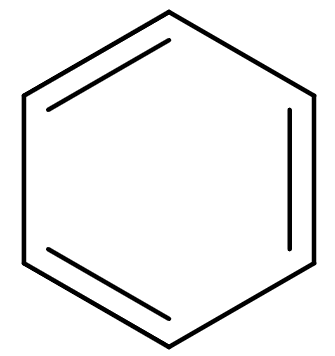
さて、芳香族に関する重要な出来事(というかこのあとの展開で欲しい出来事)を並べたわけですが、順に追っかけていきましょう。芳香族の始まりは、やはりベンゼンです。ベンゼンが単離されたあとKekuléが構造を提唱したのですが、その構造式を巡って論争があったということは有名な話でしょう。論争になった原因はその特異な性質にあります。上にも書いてありますが、ベンゼンは高い不飽和度を持つ、つまり(水素の数)/(炭素の数)が比較的小さい化合物であります。 普通、不飽和度が高い場合は二重結合を含み反応性が高い、裏を返せばそこまで安定でないと見込まれるわけですが、ベンゼンは飛び抜けて安定であった。しかも、反応を起こすにしても二重結合にありがちな付加反応はまず起こらず、置換反応を起こすのです。
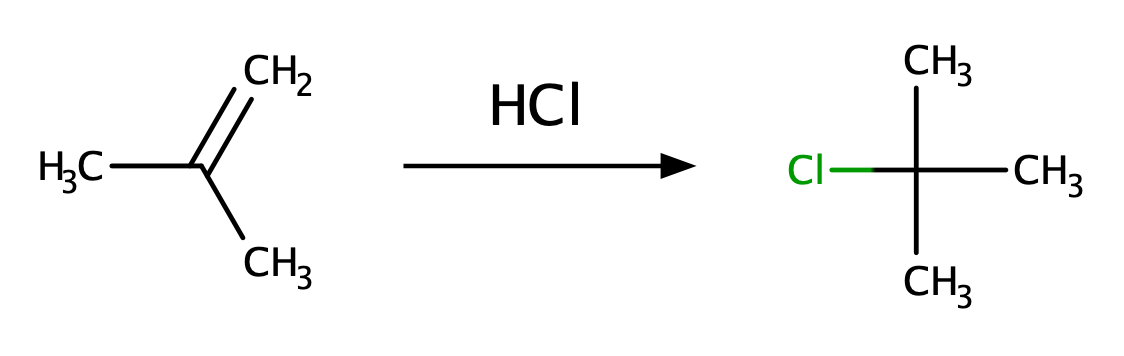
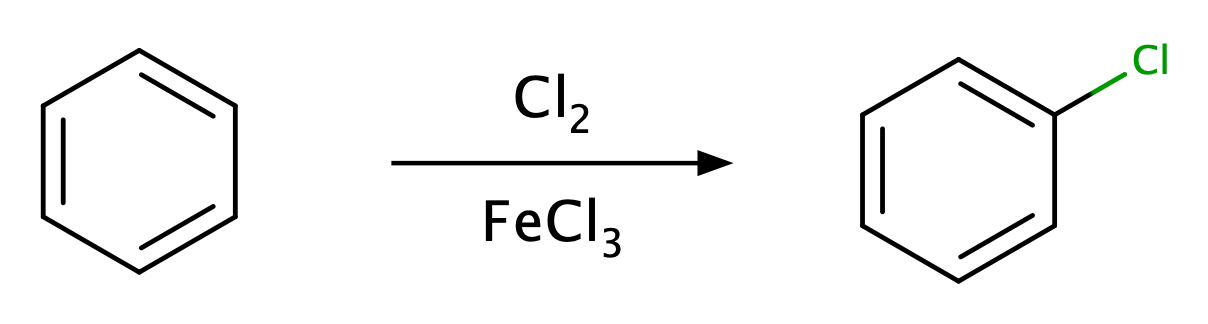
さらにKekuléの構造では単結合と二重結合が並んでいますが、それでは置換基を2個隣り合うように入れたときにできる化合物が2種存在しなければなりません。
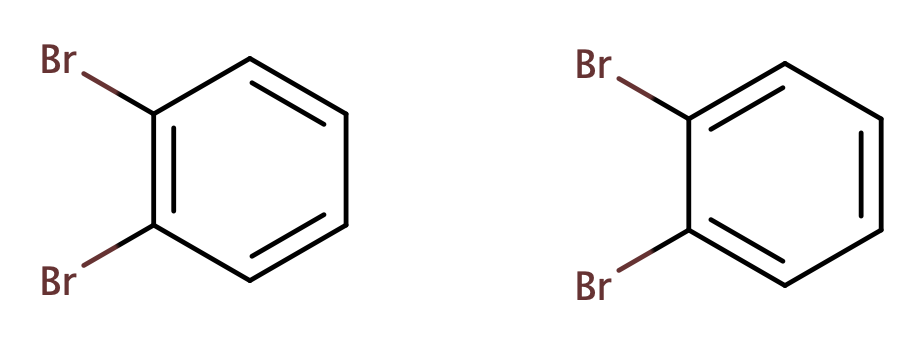
ですが、実際には1種でこの構造には不都合があるように思えます。そこでKekuléはベンゼンの単結合と二重結合の一は相互に変換し続ける平衡状態みたいな感じになっていると提案するわけです。実際にはKekuléの提案は間違っていますが、原子価結合法の共鳴という電子の非局在性についての概念につながっていくのです。
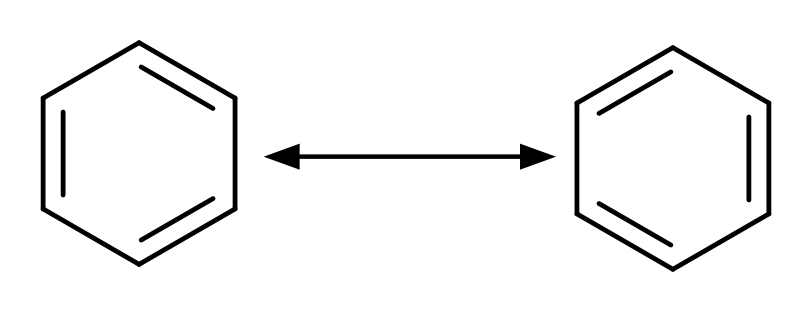
構造式を書き、電子がまるで結合の周りに局在化すると捉える。この原子価結合的な考え方に一石を投じたのがベンゼンであるわけです。ベンゼンの特異な性質を考えるときには電子の非局在性を取り入れることになるわけです。
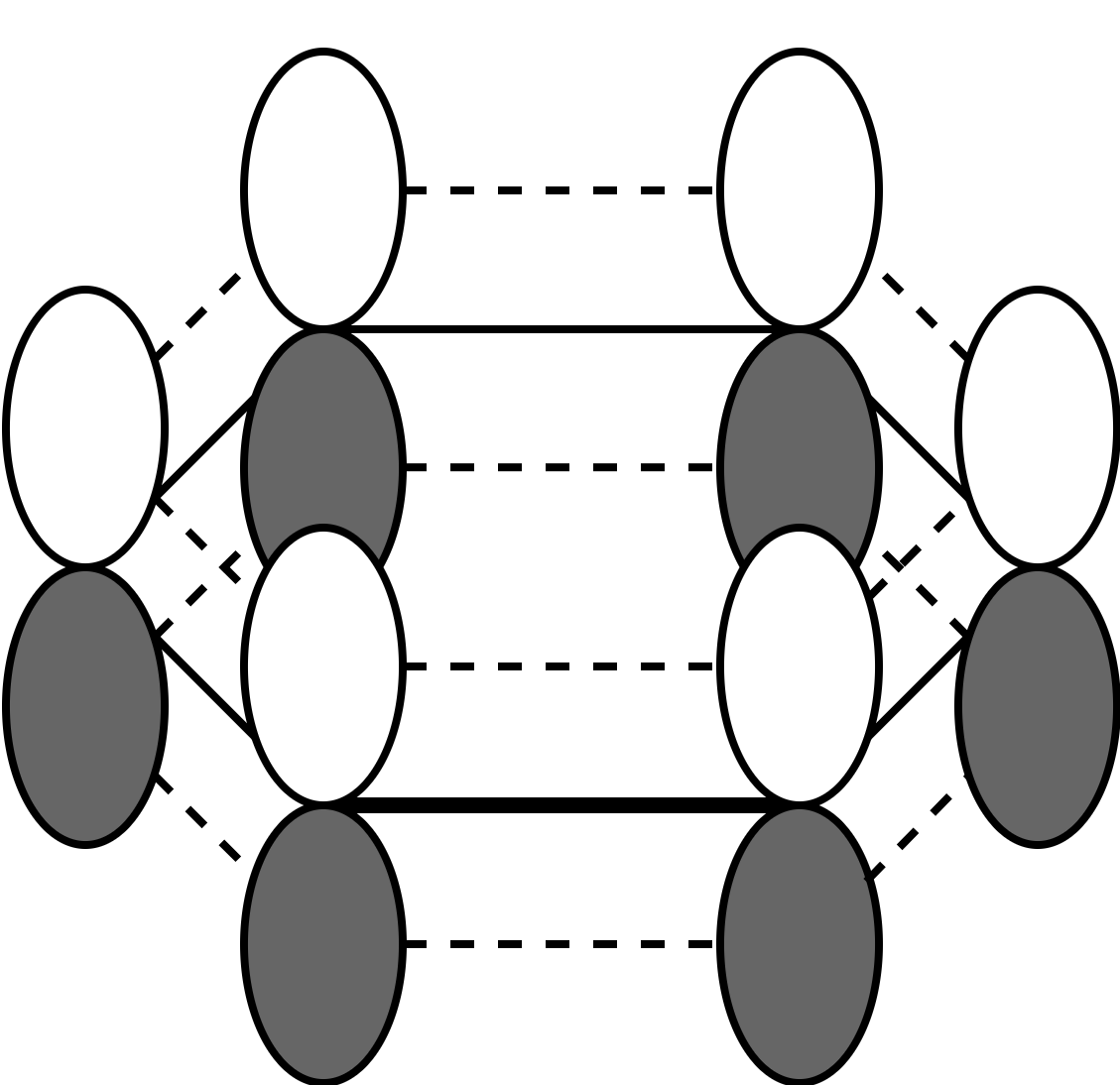
それゆえにこのベンゼンの持つ性質は特別視されるわけです。そこから芳香族という他と区別される概念が生じたのです。
ここでベンゼンの特徴的な性質をまとめておきましょう。
- 熱力学的に安定
- 付加反応ではなく求電子置換反応を起こす。
- 結合長の均等性。
- 反磁性的性質。
さらに芳香族性についての研究は進んでいきます。当然、ベンゼン環だけがこの安定性を持ちうるのか?という疑問が生じます。その疑問に対して安定性に注目して一つの明確な答えを示したのがHückelでした。詳しいことは2.2節で書きますが、Hückelは電子の非局在化を軸とする分子軌道法によるアプローチで芳香族性を示すものについての明確な答えを与えました。同時に、芳香族性とは逆に不安定化をもたらす反芳香族性という概念も登場してきます。
Hückel則提唱後の、歴史の表を見てもらったらわかると思いますが、磁気的性質について評価する手法が確立されていきます。ここまであまり磁気的性質については触れていませんでしたが、磁気的性質というのは物理学的尺度であり、反応性などといった曖昧な化学的尺度ではありません。よって現在での芳香族性の判定の重要な尺度の1つになっています。(2.3節参照)
2.2. Hückel則とは
Hückel則は有機化学の教科書において必ず登場する芳香族を予測するための法則です。 芳香族性について論じるにあたり、外すことはできない概念でしょう。 以下の4つの条件を満たすものは芳香族性を持つと予想できます。
- 分子が環構造を持っていること。
- 環構造の構成原子が全て p 軌道を持ち、かつ環構造を通じて隣接する p 軌道の接続が維持されること。
- 環の構造は平面構造。(ただし、大環状分子では完全な平面ではないこともある。)
ここまでの3条件を全て満たす化合物(一般にアヌレンと呼称)の模式図は図6の通りとなります。 並んでいるアレイ状のものが各原子の p 軌道で、ドーナツ状のリングは分子の面です。 下の図6では原子数は8となっていますが、これは一つの例であり、ここまでの話では原子数に制限は一切ありません。 (2個とか言われたらそもそも環を作れないのでダメだけど。)
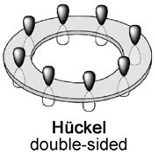
これに最後の4つ目の条件を加えます。Hückel則と呼ばれるのはこの4番目のルールですが、条件1〜3が揃って初めて意味を持ちます。
- 芳香族性は π 電子 (模式図に示している p 軌道中に入る電子) の数が$4n+2$になったときに現れる。
一方で π 電子の数が$4n$の時には反芳香族性が現れる。
電子の数で性質が一変し反対の性質が発現するというのは、不思議かもしれません。Hückel 則がどのようにして導出されたかについては第5章付録に記しているので、気になる人はご覧ください。
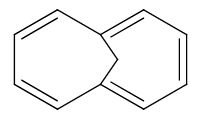
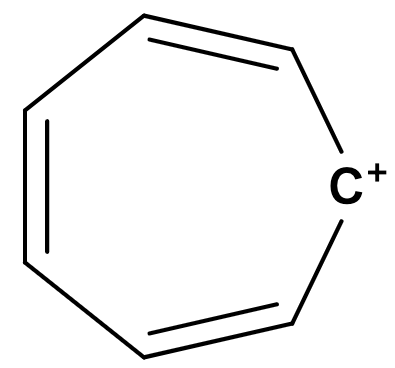
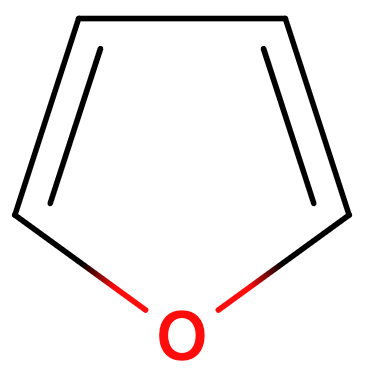
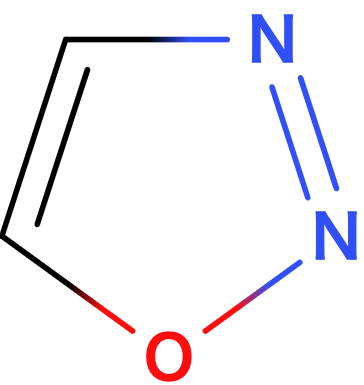
この法則によって、とても簡単に平面型アヌレンが芳香族性、もしくは反芳香族性を持つか どうかということを推測することができます。第1章の導入部分の下側によく見るタイプの芳香族性の例をいくつか載せました。これらは全てHückel則によってその芳香族性が予測される分子です。数えてみてください。一部のπ電子数を下の図7に書いておきます。環が大きくなっても、イオンであっても、ヘテロ原子があっても、これらの p 軌道中の電子を数え上げることで芳香族性であることが推測できます。
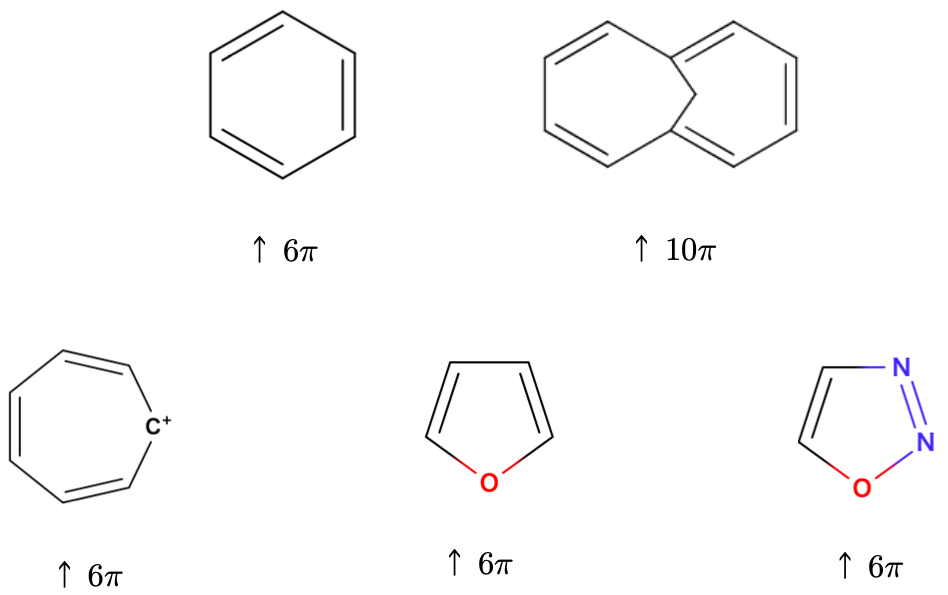
ここまでHückel則による芳香族性の判定について述べてきたわけですが、このHückel則は芳香族性を持つと予想できる化合物の一部を教えてくれるだけであります。Hückel則は平面アヌレンで非局在化による安定性を満たす化合物を探そうというモチベで導出される条件で、いわゆる芳香族性を持つ化合物を全部網羅することは目指してないわけです(まぁ目指せるわけもないよね)。ですが多くの場面で、芳香族とはHückel則を満たす化合物とされています。まぁそれで考えた方が分かりやすいし、例外的な芳香族性を語るときには「なんたら芳香族」という特別な名が与えられるので普通の文脈ではHückel則芳香族に限定しても大丈夫なわけですが、Hückel則だけを天下り的に与えられてしまうと特別な芳香族と出会ったときに脳味噌がパニックを起こすわけです、僕みたいに。こいつは誰?なんで芳香族を名乗ってる?って。そうならないために次節でHückel則よりももっと根本に存在する芳香族性についての指標を紹介しましょう。
2.3. 種々の物差し
芳香族性の主な特徴として、電子の非局在化に起因する共鳴安定エネルギー・結合長の均等化、特徴的な磁気的性質が注目されるようになったと2.1節で紹介した通りです。天才が化合物見て『これは電子が非局在化されている!芳香族!』と一発でわかれば苦労はしないのですが、そういうわけにはいかないので間接的な尺度を用いるしかないんですね。では、結合長と磁気的性質から芳香族の判定をするのに使われる尺度について1つずつ紹介させていただきます。
2.3.1. 結合長に焦点を当てる手法(HOMA)
π 電子の非局在化が進めば進むほど、構造式上の単結合と二重結合の区別が消えていき、最終的にすべての結合は同じ長さになるはずです。まさにベンゼンは理想型で、綺麗な正六角形であることが認められています。構造式上だと、長さが違うはずの単結合と二重結合が並んでいるのに。そうすると、結合の長さのばらつき度合いが小さいほど非局在化が進んでいて芳香族っぽいぞと言えそうですね。
このどれくらい芳香族よりかを示すのがHOMA(芳香族性の調和振動子モデル)という概念です。
\begin{equation} \mathrm{HOMA} = 1-\frac{\alpha}{m}\sum^m_{i}(R_{opt}-R_i)^2 \end{equation}
この式で$m$は結合の本数。$R_{opt}$は理想的な場合の結合の長さです。$R_i$が芳香族化どうか判定したい分子の結合の長さですね。得られた化合物の結晶をX線構造解析にかければ、原子の位置関係がわかるので、きっちりと測ることができます。$\alpha$は気にしなくてもいい定数です。この式がやってることは要するに、分子の結合の長さが、芳香族の理想的な長さからどれくらいばらついてるかを計算しているという程度のものです。このHOMAが1に近くなる→芳香族っぽい / 1から遠い→芳香族でない、と判断できます。
奇妙な芳香族についての章で芳香族の判定基準として登場するので紹介しました。とりあえずHOMAが1に近ければ芳香族ということだけ抑えてもらえればOKです。
2.3.2. 磁気的な性質に焦点を当てる手法(NICS)
芳香族並びに反芳香族は特徴的な磁気的性質を示します。というのもですね、下の図8のベンゼンの模式図を見てもらったらわかると思うのですが、 π 軌道が並んで、その中を π 電子がグルグル回るわけですね。これは高校物理で出てくるコイルみたいな状態だなぁと理解できるわけですね。この π 電子の流れを環電流と呼ぶのですが、環電流は外部磁場を打ち消す磁場を作るように流れるわけですね。このようにして作られた磁場というのは芳香族に特徴的で基準に取り入れることができる!というわけです。ただ、ここまでの話は古典的理解で、芳香族性の場合は説明できそうな感じですが、実は反芳香族の場合は作られる磁場の向きが逆転するという現象が起きます。
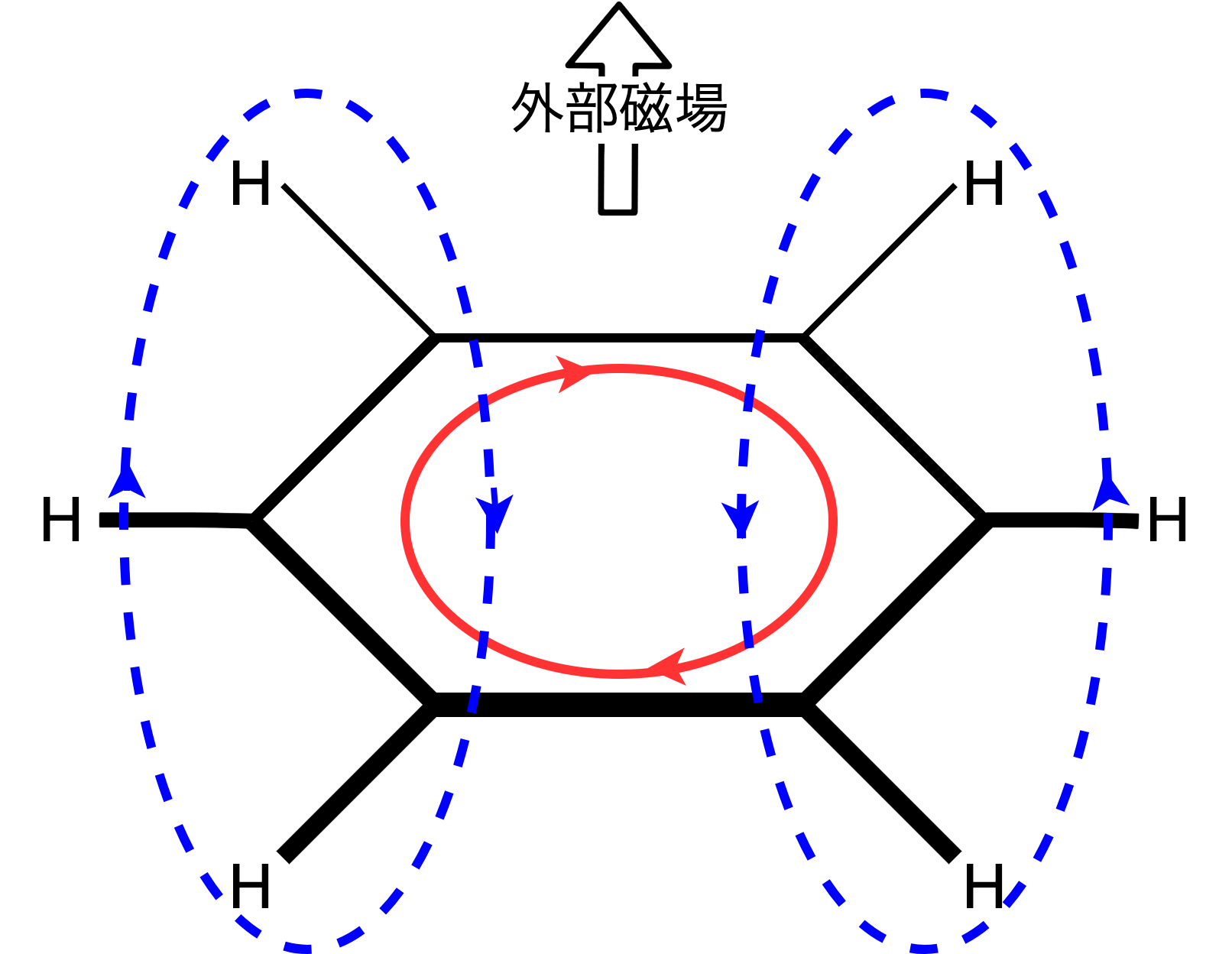
説明には量子力学を使う必要があるので(僕の理解的にも作業量的にも)険しいんですが、HOMO-LUMO差を反映しているようですね。HOMO-LUMO差が芳香族性の判定に用いられているということで、紫外可視スペクトルも芳香族に特徴的なものが現れるようですね(後の論文紹介でも出てくる)。
この磁気的性質はかなりありがたいですね〜。構造解析に多用されるNMRでモロに影響が現れます。さらにNMRで不都合な点を解決して、芳香族的な磁気的性質を見るという点で特化した手法がNICSであります。NICSでは仮想的な原子を対象の環の周りに置いて、受ける磁場を評価するんですね。仮想的原子といったところからもわかると思うのですが、これは実際の原子の位置を特定した上でそのデータを元に計算するという手法です。この手法で出てくる値が負だと芳香族、正だと反芳香族、0付近だとどちらでもないという評価をすることができます。後の論文紹介でもかなり強力な根拠として用いられているんだなぁと伝わってくるかと思います。
2.4. 総合して、現在の芳香族とは?
ここまでで色々な芳香族にまつわる概念を紹介してきたわけですが、結局のところ広い意味での芳香族性とはなんなのでしょう?
ベンゼンの特徴的とされる性質として以下の4つを上げました。
- 熱力学的に安定
- 付加反応ではなく求電子置換反応を起こす。
- 結合長の均等性。
- 反磁性的性質。
このうち、求電子置換反応についてはあまり触れてませんが、現在のところ尺度としては用いられていないようです。例えば、有名なバックミンスターフラーレン$\mathrm{C_{60}}$という、いかにも芳香族性示しそうな分子が存在するのですが、この分子は置換反応を起こしません。まぁ、結合は全部炭素炭素間結合なので、どこの結合を切るんだよという感じになるわけですが。その代わりに、付加反応は起こします。ですが、芳香族としてカウントされます。現在においては、化学的性質である反応性は芳香族の尺度としては弱いのです。その他の3つの物理的尺度を主に使用しているようですね。
芳香族という概念の一番の大元は電子の非局在性とそれに伴う安定化にあります。と言っても非局在性を直接評価するのは難しいので、その基準は3つの物理的尺度と、研究者がこれは芳香族だと信じる気持ちから構成されてる概念だと僕は理解しています。
- 熱力学的に安定
- 結合長の均等性。
- 反磁性的性質。
- 芳香族性を信じる気持ち。
3. 奇妙な芳香族
長かったですね〜。ついにタイトル回収です。2章で紹介したいわば「物差し」をもとにして芳香族かどうか判定していくのですが、その結果として芳香族に分類されている、変に思える分子についていくつか紹介させていただきます。
3.1. ホモ芳香族性
この芳香族性については簡単に紹介します。まずはHückel則のおさらいをしましょう。
- 分子が環構造を持っていること。
- 環構造の構成原子が全て p 軌道を持ち、かつ環構造を通じて隣接する p 軌道の接続が維持されること。
- 環の構造は平面構造。(ただし、大環状分子では完全な平面ではないこともある。)
- 芳香族性は π 電子の数が$4n+2$になったときに現れる。
一方で π 電子の数が$4n$の時には反芳香族性が現れる。
はい、1〜3が揃った上で4があるというのはHückel則の節で書いた通りなのですが、2については p 軌道が繋がって輪になっていることを保証するものでした。相互作用して輪になる p 軌道があれば2については破れそうだし、4の結果にあんまり影響なさそうじゃないですか?
という感じで1959年に概念が提唱されたのがホモ芳香族です。Hückel芳香族から外れたタイプの芳香族性としては一番の古株じゃないでしょうか。下の図11が実際に芳香族性が確認されているシクロオクタトリエニルカチオンというものです。出っ張ってる炭素が明かに$sp^3$混成で、 p 軌道の連続性を断ち切っているように見えますが、その両隣の炭素の p 軌道がこいつを無視して相互作用しちゃってるんですね。NMRから環電流が流れているのが確認取れているそうです。

3.2. Möbius(メビウス)芳香族
Möbius芳香族、これはなかなかインパクトのある芳香族かもしれません。Hückel則とまるっきり真逆な一般則が見出されています。Hückel則の時のように条件を書き出してみると、
- 分子が環構造を持っていること。
- 環構造の構成原子が全て p 軌道を持ち、かつ環構造を通じて隣接する p 軌道の接続が維持されること。
- Möbiusの帯と同じトポロジーを持つ環構造。
ここまでの条件を満たす化合物の模式図を書いてみると次の図12のようになります。3番目の条件がHückel則の前提条件と大きく異なる点です。
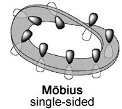
Möbius芳香族の場合、 p 軌道は少しずつ回転していきます。最終的に元の位置に戻った時に180°回転、つまり表と裏とが区別できないこと(Möbiusの帯の最たる特徴である)になります。 この180°回転することによって p 軌道の位相の逆転が起きると言うのが肝となっています。(第5章の付録参照)
ここに最後の条件を付け加えます。これがHückel則とは真逆の様相を示しているのです。この法則を以下では便宜上Möbius則と呼ばせていただきます。
- 芳香族性は π 電子の数が$4n$になったときに現れる。\\一方で π 電子の数が$4n+2$の時には反芳香族性が現れる。
Hückel則に慣れていると、なかなかに気持ち悪いですね〜。Möbius則の導出は第5章の付録に記載します。
このMöbius芳香族性、実は性質の提案自体は1964年(わかりやすく言うと前の東京五輪があった年)にE. Heilbronnerによってされていて、 割と古いものです。Hückel則と一緒に中間体やTSの安定性の議論に使われることがあるかなというところで、分子としてこの性質を見ることはほとんどないでしょう。というのも、この性質を持つ分子の合成は難しいのです。初めてMöbius芳香族の分子が合成されたと報告されたのは2003年になり、40年の空白の期間が空きます。
ここでは実際に合成された2つのMöbius芳香族化合物の例をご紹介します
3.2.1. R.HergesによるMöbius芳香族化合物の合成(2003)

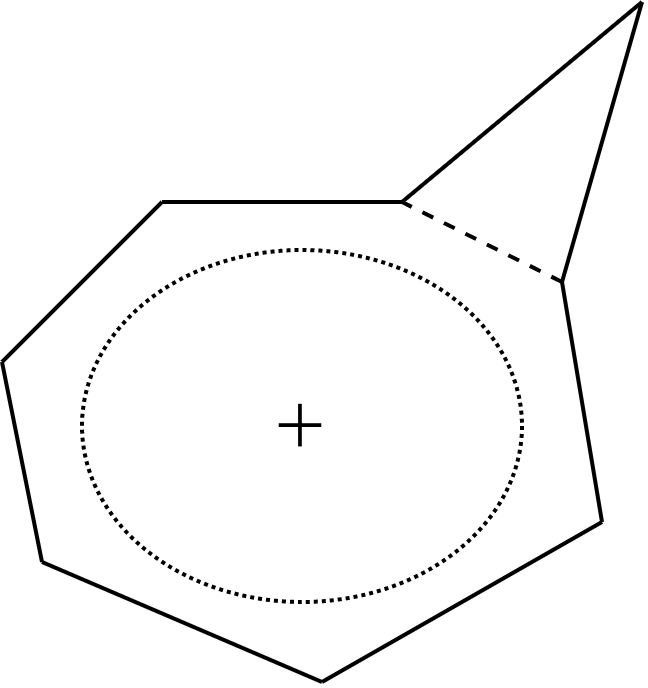
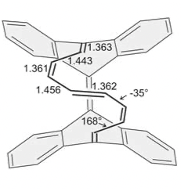
まずは、2003年にR.Herges[4]によって合成されたと初めて報告されたMöbius芳香族化合物についてご紹介します。 多分、図13をこの紙面上で見ただけで、「あ〜Möbiusの帯だ〜」とはなかなかならないと思います。僕もなりません。なった人は才能ありますよ。 X線結晶構造解析の結果得られた分子の立体的な構造は下の図14ようになります。
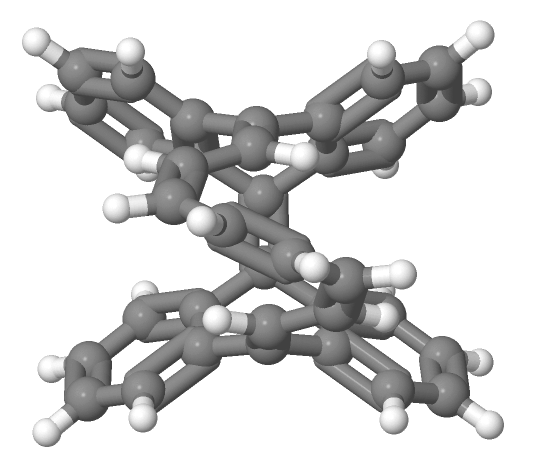
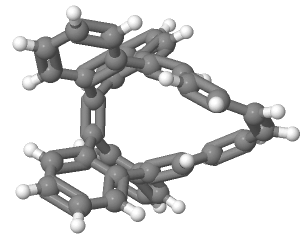
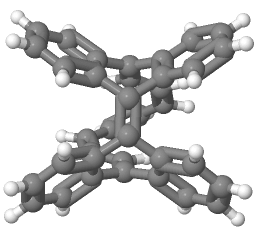
(データ出典:参考文献 [4])
多分これでも画像(この画像を引用させていただいた Access Structuresで参考文献[4]のDOIを入れていただくと、自由に動かせる3Dモデルが閲覧可能。)だし、 p 軌道が見えなくてわかりにくいと思うんですけど、手前に出てる炭化水素の帯から出てる水素(白い丸)と二重結合が含まれる面に垂直に p 軌道は飛び出しています。なので水素がなんとなくくるっと回ってるというのが認識してもらえれば、同時に p 軌道もくるっと回転していることを理解していただけるのかなと期待します。 π 電子をカウントすると16個で4の倍数になっていて、Möbius則からMöbius芳香族になりそうだなぁと推測できるわけです。
さて、有機化学の醍醐味である合成について説明しようかと思ったのですが、流石に記事が長くなりすぎるというところもあるのでHergesが用いた合成戦略のみ紹介させてもらいます。 少し前に、Möbius芳香族の提案自体は早い段階で行われていたにもかかわらず、合成は難しかったと述べました。Möbius芳香族の最大の特徴の p 軌道のねじれと p 軌道の連続性、この両方を実現した中途半端とも言える状態がMöbius芳香族には必要なわけです。ねじれによる歪みを小さくしてMöbiusトポロジーを保つためには環が大きい必要がありますが、環の炭素数が大きくなると柔らかくなった帯が簡単にフリップバックするようになります。柔らかさと剛直さが必要なわけです。そこでHergesは合成のために2つの様相の違ったパーツを組み合わせるということをします。これでMöbiusのねじれを作るのと同時にフリップバックを解消しようとしたんですね。剛直さを担保するために図13では奥側に来ている、 図14-bでは左側に来ているパーツ、つまりベンゼン環が4つ付いているパーツを用意し、そこに柔軟な帯を光反応を駆使して接続しました。いくつかの異性体ができますが、そのうちの一つがここで紹介しているMöbius芳香族化合物なのです。(図15)
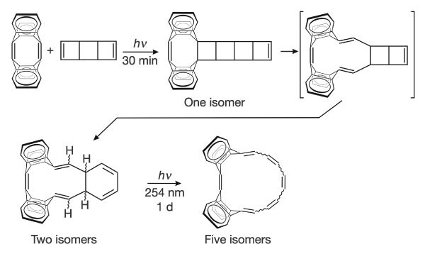
ところで、この化合物の芳香族性はどのように確認されたのでしょうか。論文中でHergesは結合長の均等性と安定化エネルギーを根拠にして芳香族性の発現を主張しています。結合長の均等性を示す指標であるHOMAは0.35であり$\mathrm{C_{60}}$中のベンゼン環の値に近しいものです。論文([4])を見た感じ磁気的性質での判定はなさそうなんですよね、次に紹介する大須賀教授の論文(参考文献[6])にはこの化合物のNICSの値的には微妙な芳香族性だというような記述があります。
3.2.2. 大須賀教授によるMöbius芳香族化合物の合成(2008)
次に2008年に京都大学の大須賀教授らによって合成、Möbius芳香族性が確認された化合物[6]について紹介させていただきます。

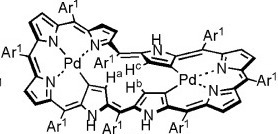
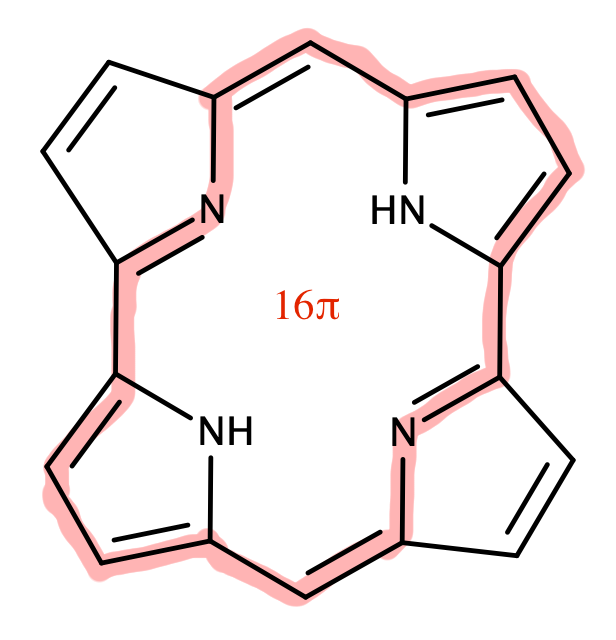
大須賀教授はポルフィリン(図17)について研究を進められてきた先生で、拡張ポルフィリンを用いた見事な戦略で先に挙げたMöbius芳香族合成の難しいポイントをクリアしています。しかもその汎用性の高さから、Möbius芳香族化合物を一つのみならず、複数作成していらっしゃいます。参考文献[6]においても$36\pi$、$32\pi$、$28\pi$の化合物の合成と、それぞれの芳香族性についての評価が報告されています。図16は$36\pi$のMöbius芳香族化合物です。
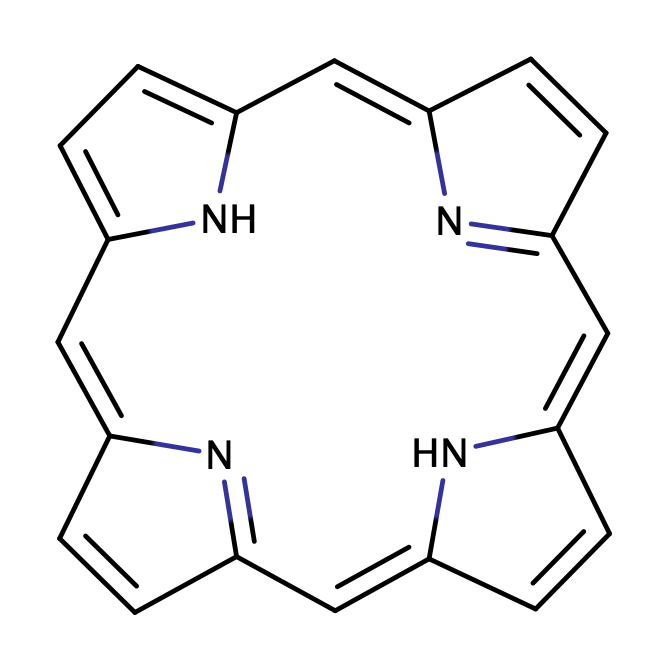
拡張ポルフィリンのアドバンテージとして以下の4つが参考文献[6]において示されています。
- 全体的な構造の柔軟さ。
- ポルフィリンを構成する部品であるピロールが状況によって反転することができる。
- 二電子の酸化還元に対する受容性の高さ。
- ポルフィリン中のNやCを金属に配位させることで、配座の固定をすることができる。
そう、1・2・4でMöbius芳香族に必要な柔軟さと剛直さを担保することができるのです。さらに3から π 電子の数を操作することも可能になってくるというわけです。

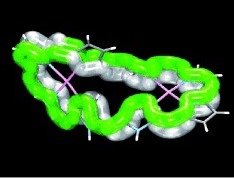
(出典:参考文献 [6])
上の図から、滑らかに π 軌道がねじれて緑色と白色が反転して結合されているのがはっきりとわかると思います。まさにMöbiusの帯となっているわけです。
論文中での芳香族性の判定にはNMRやNICSといった磁気的性質、また紫外可視吸収スペクトルを判断材料としていますね。NICSは負の値を示していて、なるほどこれは芳香族だと判定できるわけです。
3.3. 三次元芳香族
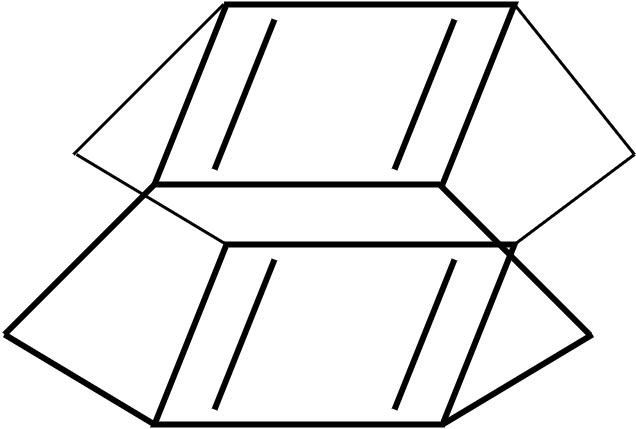
3次元的な構造を持った芳香族化合物というものはフラーレンなどいろいろあると思うのですが、ここで紹介するのは2次元の反芳香族化合物を積層させることで得られる3次元的な芳香族化合物について紹介します。イメージ的には下の図のような感じですね。

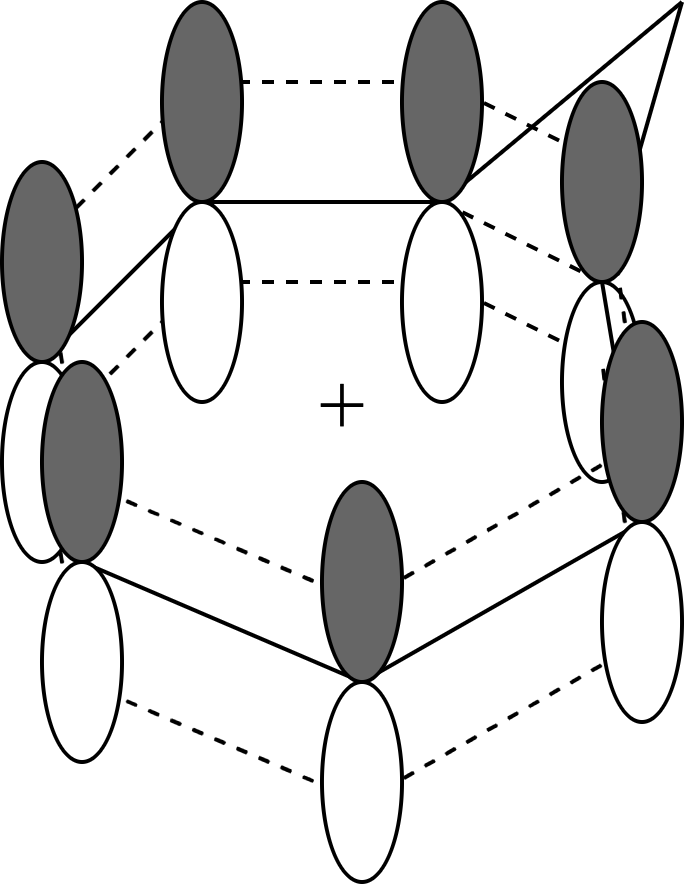
これで芳香族性を持つというのは意味がわからんと思います。どうやら一枚一枚の p 軌道がお互いに相互作用することによって、新たな性質が生まれているようですね。(下図19参照)
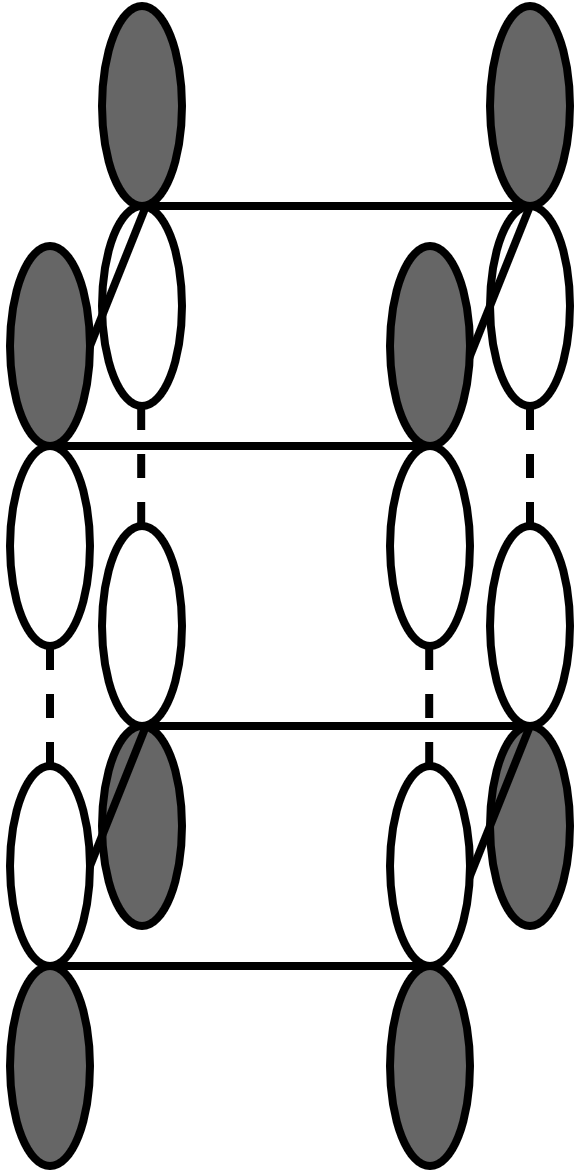
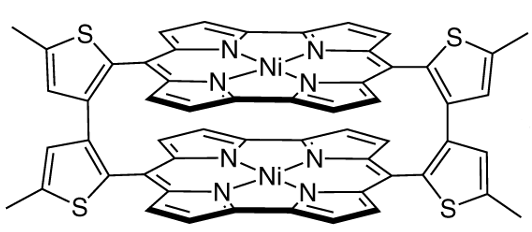
まぁこんな分子は π 軌道が相互作用しようが、歪みがエグ過ぎてとんでもなく不安定そうですよね。そんなわけで合成できていないのですが、2019年に名古屋大学の忍久保教授らが合成された本物の化合物を紹介させていただきます。忍久保教授はノルコロール(図20)というポルフィリンに似た反芳香族化合物の合成に成功されています。
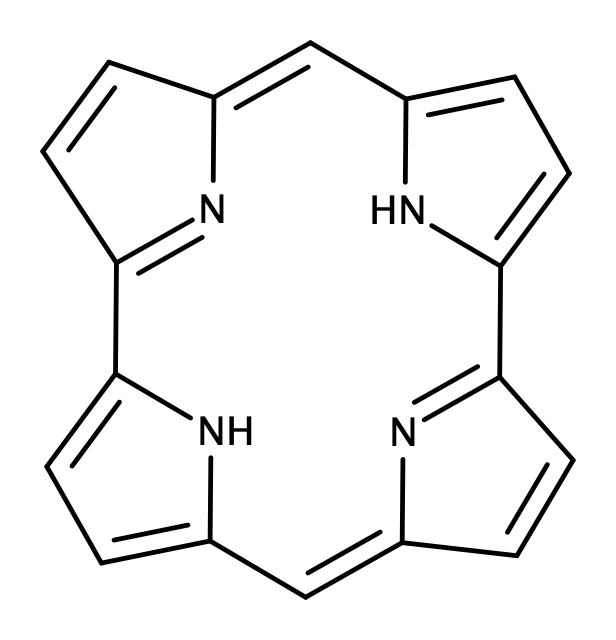
このノルコロールのニッケル錯体を2つ重ねることで、芳香族性が生じるのか検証をなされています。その分子は以下の通りです。

二枚のノルコロールが若干(20°ほど)ずれた上で、両方とも平面構造を保っています。平面を保っているという事実は二枚のノルコロールの間に引力が働いているということを意味していて、二枚のノルコロールの電子の安定化相互作用があることがわかります。(ベンゼンなどは電子間反発などのため、平面にならない。)さらにNICSも芳香族性を支持している上、論文の中で忍久保教授らは分子中の電流を計算するということをしています。その結果、二枚のノルコロールの間の空間中でも電子のやりとりがあり、かつニッケルの存在がこの効果を高めていると報告されています。なんというか、とても好奇心をそそられる図が掲載されているので、ぜひ参考文献[8](Open Access)をご覧ください。
3.4. その他
ここまで奇妙な芳香族と、論文中でどのようにして芳香族認定をいただいているのかということを紹介してきたのですが、時間と体力の限界が来てしまいました。なので紹介しきれなかった(のと自分が理解できてない)ものをここで概念だけ紹介しておきます。これまで紹介したのはすべて π 軌道が主役でした。しかし、$\sigma$軌道の芳香族性も報告がされているようです。また、前の節で紹介した3次元の芳香族化合物は2次元を積み重ねたものでしたが、$o$-カルボランという化合物は球体的な構造中に π 電子が非局在化して芳香族性を示すらしいです。よく知りませんが。 さらに興味深いのはここまでの芳香族性はすべて基底状態での話だったのですが、励起状態での芳香族性を考えるということも行われていて、Baird芳香族というものもあるようです。どうやら$4n\pi$のときに安定化があるようで、もうよくわかりませんね。この芳香族性は平面での共役系である必要があるのですが、じゃあMöbiusトポロジーで励起状態だったら$4n+2\pi$でこれまた芳香族性が出るのかしらとか妄想したりしてます。
4. 最後に
このような長文を最後まで読んでいただきありがとうございました。 前置きからとてつもなく長々と書いてしまって、申し訳ないなぁという気持ちはあるのですが、変な芳香族を紹介するには芳香族ってどう決めるの?というところに突っ込まないと良くない気がしたので許してください。後半の変な芳香族についてはやはり変だから、実際の化合物の例って少なくて体系的に語るのって難しいんですよね。だから少ない合成例についてのいくつかの論文を直接探って芳香族と言える根拠は何かというのを具体的に探って紹介するという道を取りました。もちろんのことながら、元々の論文を読むととても勉強になる(僕が理解できないから触れてない場所とか)ので、なにこれ〜ってなった分子があれば、ぜひ参考文献から元の論文に当たってください。書いている人間は参考文献をふらふらになりながら読み込んで書いている一介の学生なので、間違っているところがあるかもしれません。やばい記述があれば指摘いただければ幸いです。ではこれで終わりとします。疲れた〜。
5. 付録
この章は付録ということで別に読まなくてもいいんですが、一応Hückel則とMöbius則の導出的なものを載せておいた方が感動的かなと思ったので、追加しました。量子化学の内容になっていますので、一応LCAO近似の説明から載せはしますが、量子化学の根本的な考え方の解説まではしません。教科書作るつもりはないので。
5.1. LCAO近似と永年方程式
一般に、ハミルトニアン$\hat{H}$に対する固有関数$\psi_0$とその固有値$E_0$は次のシュレディンガー方程式を満たします。
\[ \hat{H}\psi_0=E_0\psi_0 \]
この式の左から$\psi_0^{*}$を掛けて全空間で積分すると、以下の式を得ます。
\[ E_0=\frac{\int \psi_0^*\hat{H} \psi_0 d\tau}{\int\psi_0^{*} \psi_0 d\tau} \]
ここで、$\psi_0$の代わりに任意の関数$\phi$をこの式に代入すると、
\[ E=\frac{\int \phi^{*}\hat{H} \phi d\tau}{\int\phi^{*} \phi d\tau} \]
となり、常に$E \geq E_0$となることが知られています。ここで、ある分子の軌道$\phi$を、それを構成する原子の軌道$\chi_i \ (i=1,2,\cdots,n)$の線形結合
\[ \phi = \sum_{i=1}^n c_i \chi_i \]
で表すことを考えてみましょう。これを{\bf LCAO近似}と呼びます。このとき求めたいのは$E$の最小値なので、
\[ \frac{\partial E}{\partial c_i}=0 \qquad \frac{\partial E}{\partial c_i^*}=0 \qquad (i=1,2,\cdots,n) \]
を満たす$c_i \ (i=1,2,\cdots,n)$を求めれば良いことになります。計算をすると、
\begin{equation} \sum_{j=1}^n c_j (H_{ij}-ES_{ij})=0 \qquad (i=1,2,\cdots,n)\label{eq:sum} \end{equation}
の$n$個の連立一次方程式が得られ、これを解くことで$c_i \ (i=1,2,\cdots,n)$が求まります。
ここで、
\begin{align} H_{ij}&=\int\chi_i^*\hat{H}\chi_j d\tau \label{eq:Hij}\\ S_{ij}&=\int\chi_i^*\chi_j d\tau \label{eq:Sij} \end{align}
であります。
式2は行列を用いた形式で書くと以下のようになります。
\[ \begin{pmatrix} H_{11} - ES_{11} & H_{12} - ES_{12} & \dots & H_{1n} - ES_{1n} \\ H_{21} - ES_{21} & H_{22} - ES_{22} & \dots & H_{2n} - ES_{2n} \\ \vdots & \vdots & \ddots & \vdots & \\ H_{n1} - ES_{n1} & H_{n2} - ES_{n2} & \dots & H_{nn} - ES_{nn} \\ \end{pmatrix} \begin{pmatrix} c_1 \\ c_2 \\ \vdots\\ c_n\\ \end{pmatrix} =0 \]
式2がちゃんとした解を持つためには以下の行列式が成立している必要があります。
\begin{equation} \mathrm{det} \begin{pmatrix} H_{11} - ES_{11} & H_{12} - ES_{12} & \dots & H_{1n} - ES_{1n} \\ H_{21} - ES_{21} & H_{22} - ES_{22} & \dots & H_{2n} - ES_{2n} \\ \vdots & \vdots & \ddots & \vdots & \\ H_{n1} - ES_{n1} & H_{n2} - ES_{n2} & \dots & H_{nn} - ES_{nn} \\ \end{pmatrix}=0 \label{eq:permanent} \end{equation}
式5を指して{\bf 永年方程式}と呼びます。
5.2. Hückel則の導出
ついにHückel法を用いたHückel則の導出を行おうと思います。 Hückel法とは、炭化水素の π 軌道のMOとそのエネルギーを求めるための永年方程式(式5)を極端に単純化するために、Hückelが提案したHückel近似を用いて計算する方法です。
Hückel近似を適用する前に一つ重要な前提があります。それは π 軌道と$\sigma$軌道とは対称性の違いから混じり合うことがなく、 π AO (AOとはAtomic Orbital、つまり原子軌道の略。)のみを抽出してLCAO MOを作ることが許されるというものです。よって π AOのみ考えることで前節の方法で π 軌道を求めることができるのですが、ここでHückel近似を適用します。
Hückel近似は次の2つの近似からなります。ただし、以下では$\chi_\mu$は炭素原子$\mu$の π AOとし、炭素原子は$m$個存在するとします。
(1)$H_{\mu\nu}$(式3)についての近似
- $\mu = \nu$のとき、$H_{\mu\mu}$はすべての炭素原子上で同じ値をとると仮定。$H_{\mu\mu}= \alpha$とする。
- $\mu \neq \nu$のとき、
原子$\mu$と原子$\nu$が直接結合しているとき、$H_{\mu\nu}=\beta$と置く一方、
原子$\mu$と原子$\nu$が直接結合していないときは$H_{\mu\nu}=0$とおく。
(2)$S_{\mu\nu}$(式4)についての近似
\[ S_{\mu\nu}=\int\chi_\mu^*\chi_\nu d\tau=\delta_{\mu\nu} \]
つまり、$\mu = \nu$のとき$S_{\mu\nu}=1$、$\mu \neq \nu$のとき$S_{\mu\nu}=0$。
この近似を適用すると、LCAO近似から求められた式2は以下のようになります。
\[ (\alpha - E)c_{\mu}+ \sum_{\nu(\mu \rightarrow \nu)} \beta c_{\nu} =0 \qquad (\mu=1,2,\cdots,m) \]
この式では特殊な記号$\sum_{\nu(\mu \rightarrow \nu)}$を使っていますが、これは原子$\mu$と直接結合する原子$\nu$についてのみ足し上げるという操作を指示しています。
さらに単純化することができ、$E = \alpha + \lambda \beta$とすることで次の式が導けます。
\begin{equation} -\lambda c_{\mu}+ \sum_{\nu(\mu \rightarrow \nu)} c_{\nu} =0 \qquad (\mu=1,2,\cdots,m) \label{eq:sum2} \end{equation}
では次に実際の分子でHückel法を適用してみて、永年方程式を導出して解いてみましょう。 芳香族の基本中の基本であるところのベンゼンで考えてみましょう。
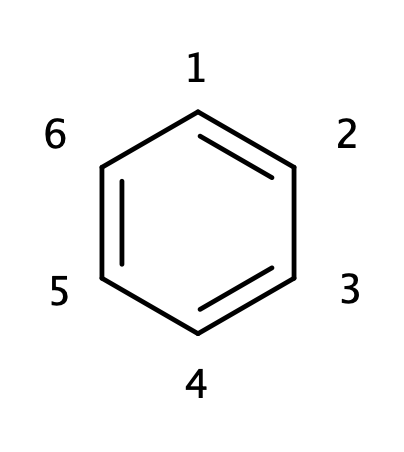
上のようにベンゼンの炭素に対して番号を振ります。 炭素1について考える、つまり$\mu=1$とします。炭素1が直接結合するのは炭素2と6なので、式\ref{eq:sum2}から、
\[ -\lambda c_{1}+ c_{2} + c_{6} =0 \]
となります。行列で表現すると、
\[ \begin{pmatrix} -\lambda & 1 & 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} c_1 \\ c_2 \\ c_3 \\ c_4 \\ c_5 \\ c_6 \\ \end{pmatrix} =0 \]
これを$\mu=2〜6$についても考えることで、下の行列式が完成します。
\[ \begin{pmatrix} -\lambda & 1 & 0 & 0 & 0 & 1 \\ 1 & -\lambda & 1 & 0 & 0 & 0 \\ 0 & 1 & -\lambda & 1 & 0 & 0 \\ 0 & 0 & 1 & -\lambda & 1 & 0 \\ 0 & 0 & 0 & 1 & -\lambda & 1 \\ 1 & 0 & 0 & 0 & 1 & -\lambda \\ \end{pmatrix} \begin{pmatrix} c_1 \\ c_2 \\ c_3 \\ c_4 \\ c_5 \\ c_6 \\ \end{pmatrix} =0 \]
これに対応する永年方程式(式5)は以下の通りです。
\[ \mathrm{det} \begin{pmatrix} -\lambda & 1 & 0 & 0 & 0 & 1 \\ 1 & -\lambda & 1 & 0 & 0 & 0 \\ 0 & 1 & -\lambda & 1 & 0 & 0 \\ 0 & 0 & 1 & -\lambda & 1 & 0 \\ 0 & 0 & 0 & 1 & -\lambda & 1 \\ 1 & 0 & 0 & 0 & 1 & -\lambda \\ \end{pmatrix} =0 \]
Hückel法使うと、永年方程式中が0だらけで嬉しい!ってなるわけですね。 展開すると、
\[ (\lambda^2 -1)^2 (\lambda^2 -4)=0 \]
よって、
\[ \lambda=\pm 1,\mp 2 \]
が得られるのであります。さらに言うと、$\lambda=\pm 1$は重根となるので、二重に縮重した軌道が得られます。
始めに例として具体的にベンゼンを解いたわけでありますが、一般のアヌレンについてはどうなるのでしょうか。n個の炭素を含んだアヌレンについてベンゼンと同様に考えていくと、次のような永年方程式が得られます。
\[ \mathrm{det} \begin{pmatrix} -\lambda & 1 & & & & 1 \\ 1 & -\lambda & 1 & & & \\ & 1 & \ddots & \ddots & & \\ & & \ddots & \ddots & 1 & \\ & & & 1 & -\lambda & 1 \\ 1 & & & & 1 & -\lambda \\ \end{pmatrix} =0 \]
わかりづらくなるので、0は全部空白にしています。この式は$n\times n$行列式です。これは巡回行列と言う特殊な形の行列となっています。これは一般の整数$n$に対して次のような解を持ちます。
\[ \lambda_k=2\cos\frac{2\pi k}{n} \]
$k$は$0, \pm1, \pm2,\dots$であり、n個存在します。$\lambda$だとわかりにくいので、$E = \alpha + \lambda \beta$の関係式から元のエネルギー$E$に戻しましょう。
\[ E_k=\alpha+2\beta\cos\frac{2\pi k}{n} \]
これ、実はめちゃくちゃわかりやすい式となっています。 例えばベンゼンのエネルギーダイヤグラムを書いてみましょうか。
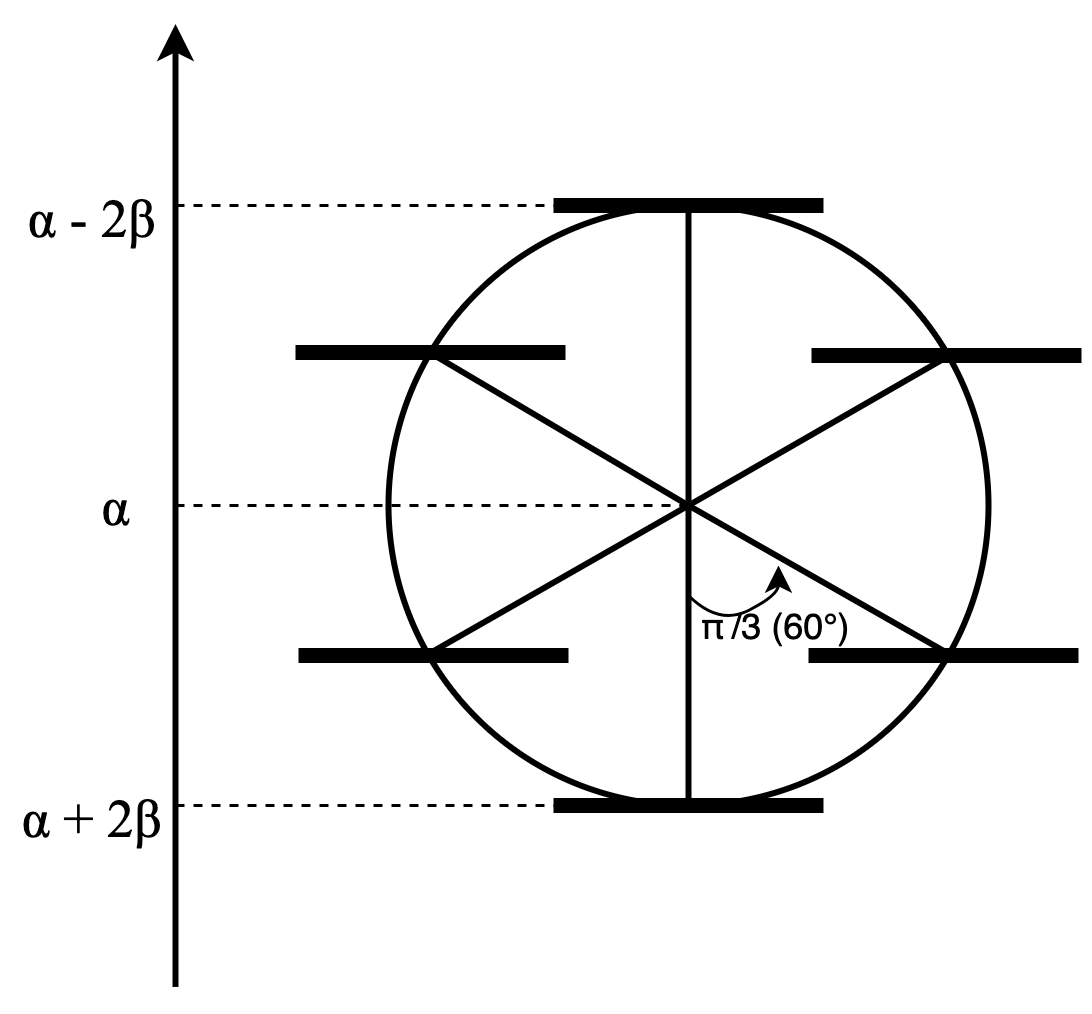
このように、中心の高さが$\alpha$で半径が$2\beta$の円をまず書きます。中心から真下に半径を書き入れて、円と交わったところが一番エネルギーの低い軌道です。そこから$2\pi/n$ずつずらした半径を書き入れて円と交わったところが軌道となります。高さをみてやるとすぐに軌道のエネルギーがわかるんですね。もっと早い話が、正$n$角形の一つの頂点が一番下に来るようにしたら、頂点の位置が軌道ですよってことです。このようにして書けるダイアグラムをフロストの円と呼びます。
では、軌道に電子を入れてみましょう。
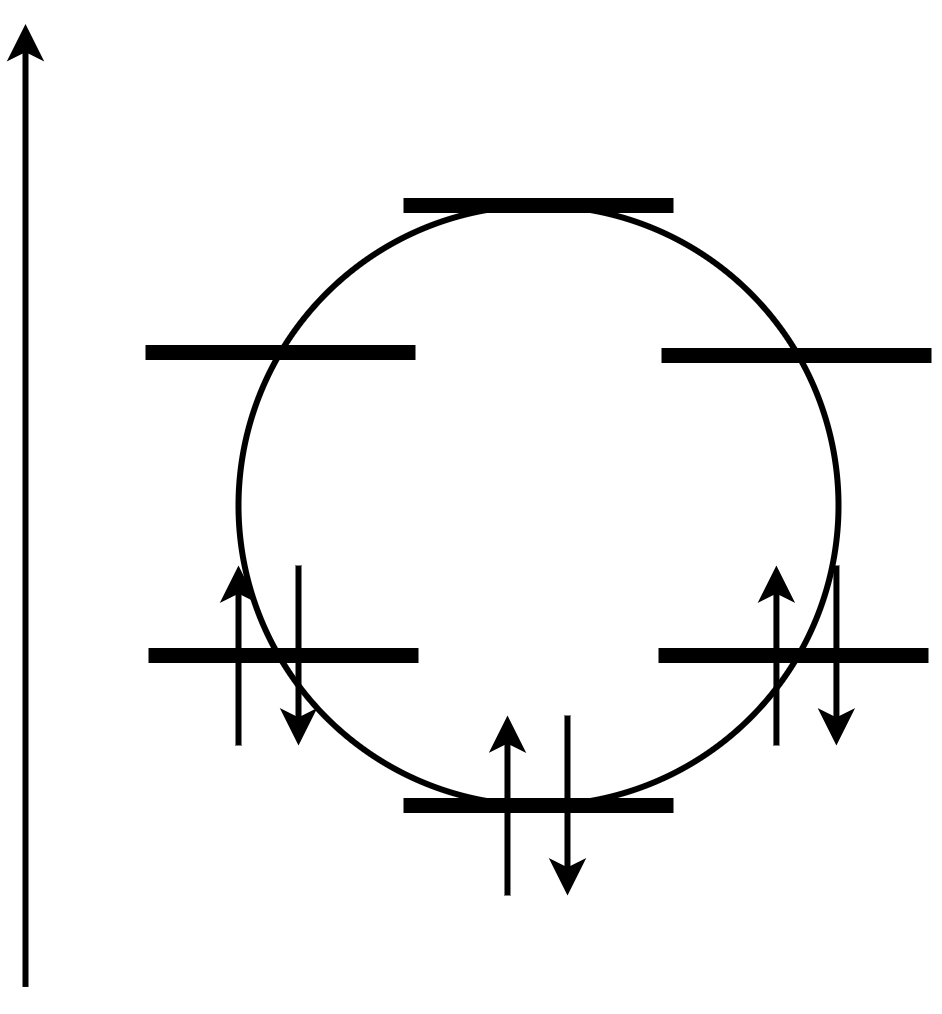
いい感じにエネルギーが低い軌道が埋まりきっているんですね。このエネルギーの下がり具合が芳香族の安定性の理由なのです。同じ数の炭素原子を持つ鎖状共役ポリエンと比べてもでかいです。さらにHOMO-LUMO差がとても広くなっています。
ところで、ベンゼンの場合は6、つまり$4n+2\pi$でしたが、$4n\pi$の場合はどうなるのでしょうか?4つの炭素原子を持つアヌレンで見てみましょう。
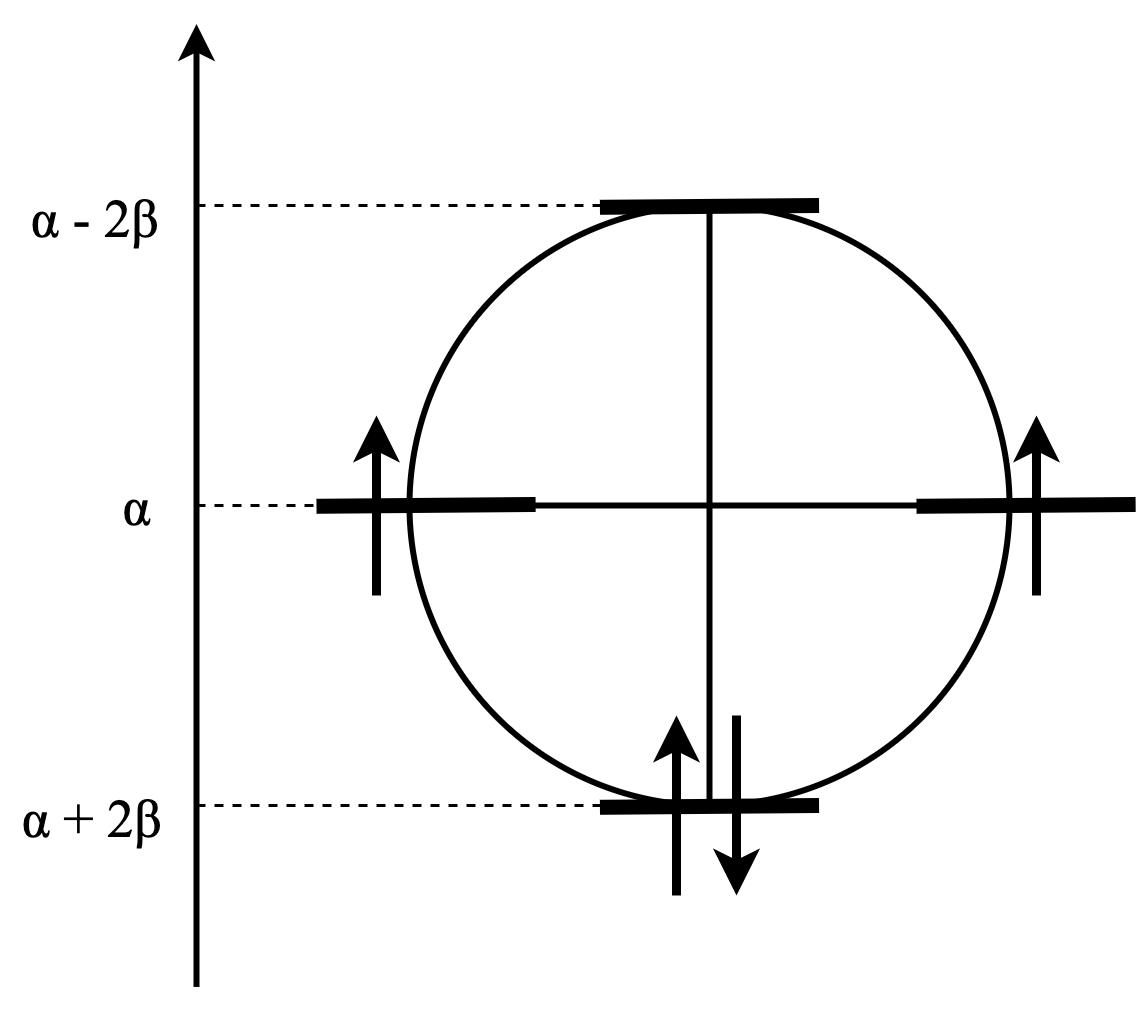
このように不対電子ができます。これはあんまり嬉しくないんですね。さらに共役鎖状ポリエンと比べても安定化分は少ないです。よって、安定化のためにちょっと形が歪んだり、そもそも平面じゃなくして π 共役系を断ち切ったりします。またHOMO-LUMO差が微小になります。
このようにしてHückel則が出てくるわけですね。
5.3. Möbius則の導出
もう疲れてるので、手短に行きます。対象とする分子は次のベンゼンに似た分子なのですが、Möbiusトポロジーを持っていて、赤線が引いてある1と6の間で位相の反転が起きていると認識してください。Möbiusベンゼンとでも呼びましょうか。
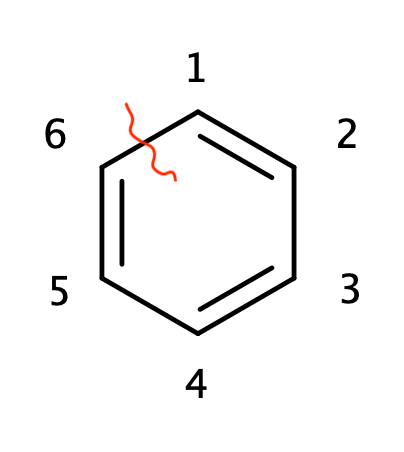
Hückelの時と同じように永年方程式をたてます。
\[ \mathrm{det} \begin{pmatrix} -\lambda & 1 & 0 & 0 & 0 & -1 \\ 1 & -\lambda & 1 & 0 & 0 & 0 \\ 0 & 1 & -\lambda & 1 & 0 & 0 \\ 0 & 0 & 1 & -\lambda & 1 & 0 \\ 0 & 0 & 0 & 1 & -\lambda & 1 \\ -1 & 0 & 0 & 0 & 1 & -\lambda \\ \end{pmatrix} =0 \]
Hückel則の時ととてもよく似てますが、位相の反転が起きる炭素1-6間では符号の逆転が起きます。
この結果、以下のようなエネルギーダイアグラムがかけます。
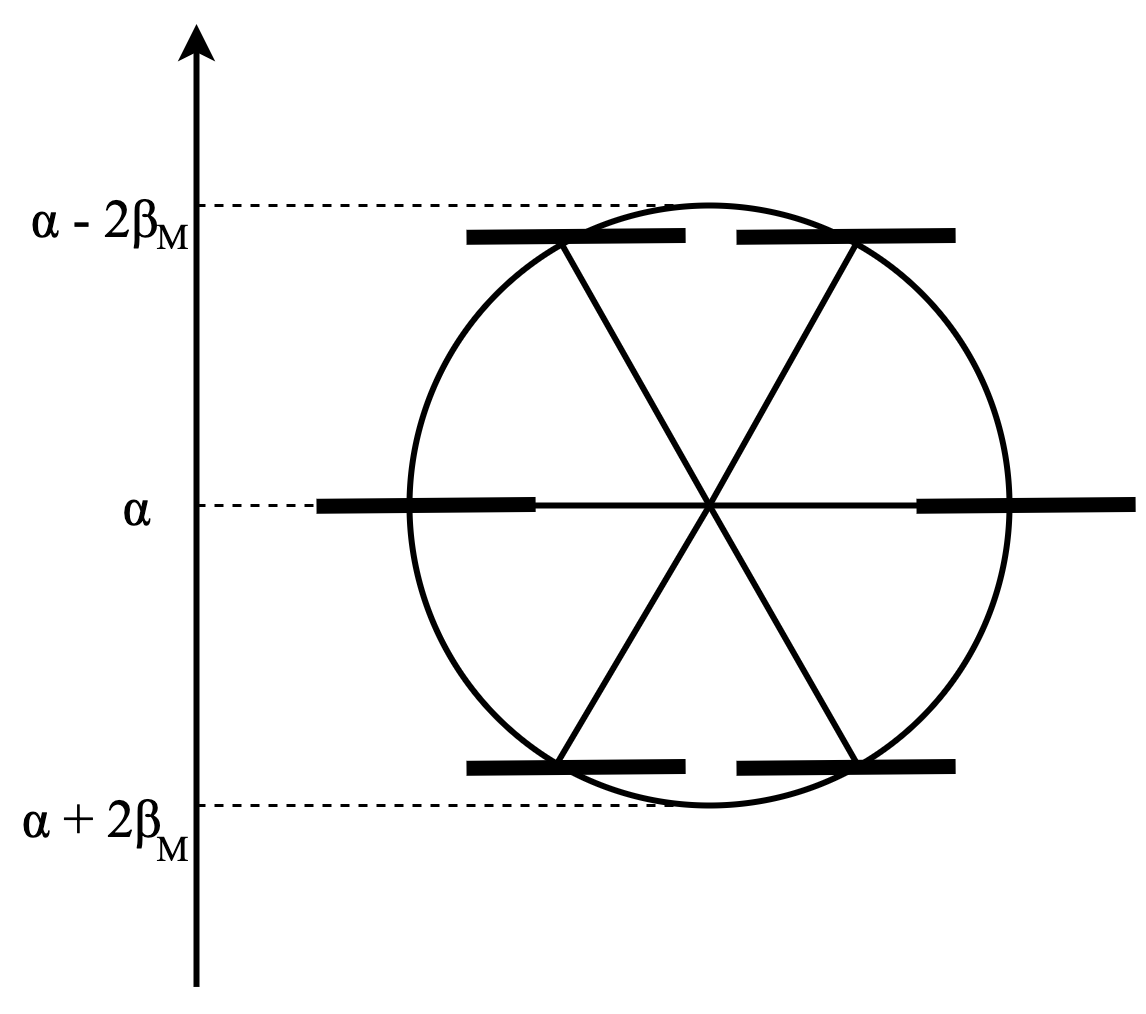
この図25を見たらめちゃくちゃHückelの時と似てることに気づくと思います。Möbius芳香族の場合の$E_k$は以下の通りです。
\[ E_k=\alpha+2\beta_M\cos\frac{(2k+1)\pi}{n} \]
Möbiusの場合も一般的にHückelと同じように円を書いて、正$n$角形書いてたら良いんですね。
ただ違う点があって、それは$\beta$の大きさと、正$n$角形の辺の一つを水平になるようにして一番エネルギー的に低い位置に持ってくるということです。軌道の重なりに対応する$\beta$は平面アヌレンとの区別のために、$\beta_M$と書いています。
もう、お分かりかと思うのですが、$4n$の方がMöbiusトポロジーのアヌレンにはありがたそうですよね?よってMöbius則が出てくるわけです。
参考文献
[1] 中筋一弘・久保孝史・鈴木孝紀・豊田真司 『構造有機化学 基礎から物性へのアプローチ まで』東京化学同人 2020
[2] 原田義也 『量子化学 上巻』裳華房 2007
[3] Maitland Jones Jr., Steven A Fleming. Organic Chemistry–Fifth Edition. WW Norton & Co, 2013.
[4] Ajami D, Oeckler O, Simon A, Herges R. Synthesis of a Möbius aromatic hydrocarbon. Nature. 2003 Dec 18;426(6968):819-21. doi: 10.1038/nature02224. PMID: 14685233.
[5] von Schleyer, P., & Jiao, H. (1996). What is aromaticity?, Pure and Applied Chem- istry, 68(2), 209-218. doi: https://doi.org/10.1351/pac199668020209
[6] Tanaka, Y., Saito, S., Mori, S., Aratani, N., Shinokubo, H., Shibata, N., Higuchi, Y., Yoon, Z., Kim, K., Noh, S., Park, J., Kim, D. and Osuka, A. (2008), Metalation of Expanded Porphyrins: A Chemical Trigger Used To Produce Molecular Twisting and Möbius Aromaticity. Angewandte Chemie International Edition, 47: 681-684. doi:10.1002/anie.200704407
[7] E. Heilbronner, Hückel molecular orbitals of Möbius-type conformations of annulenes, Tetrahedron Letters, Volume 5, Issue 29, 1964, Pages 1923- 1928, ISSN 0040-4039, https://doi.org/10.1016/S0040-4039(01)89474-0. ( http://www.sciencedirect.com/science/article/pii/S0040403901894740)
[8] Nozawa, R., Kim, J., Oh, J. et al. Three-dimensional aromaticity in an antiaromatic cyclophane. Nat Commun 10, 3576 (2019). https://doi.org/10.1038/s41467-019-11467-4
[9] S. Winstein Journal of the American Chemical Society 1959 81 (24), 6524-6525 DOI: 10.1021/ja01533a052